全流程Pose Driver Deformer

概要

根据主骨骼当前旋转角和Targets旋转角，插值出Blendshape权重或次级骨骼Transform

使用RBF插值，把Rm（旋转维度） ==> Rn（Target数量）, 优点：平滑曲线、可以控制每个插值点的影响范围，既能做到局部影响也能做到全局影响

分解旋转为轴向（Twist）和非轴向（Orientation）

调研技术方案

针对一个rig，在旋转某些骨骼时会导致蒙皮mesh出现不自然的状况（比如手肘转动带动肌肉、弯腰带动衣服）。此时对mesh的修正主要有两种思路：

blendshape：创建多个target，每个target有一个权重，动画师调整这些target的权重曲线（key帧帧间B-Spline插值）。缺点：需要存储很多Mesh顶点信息，无论是内存还是计算时间开销都更大
次级骨骼：为需要的主骨骼添加多个次级骨骼，制作动画时，key好主骨骼之后，再key次级骨骼的Transform。

这两种的共同点是：

主骨骼旋转需要调整Mesh，需要动画师去编辑Mesh或编辑次级骨骼间接编辑Mesh。
在key的动画的过程中实现编辑Mesh，对于新的动画无法复用。

引入PSD，根据主骨骼旋转位置，插值出blendshape权重或次级骨骼Transform。在maya中使用手柄拖动时也能看到调整Mesh的生效，制作动画时只需要key主骨骼关键帧即可。

方案：在游戏流水线中引入基于骨骼的PSD流程，打通 Maya/MotionBuilder/Unreal/Max

Reference:

J.P.Lewis. Pose Space Deformation: A Unified Approach to Shape Interpolation and Skeleton-Driven Deformation, http://scribblethink.org/Work/PSD/PSD.pdf
EigenSkin: Real Time Large Deformation Character Skinning in Hardware(https://zhuanlan.zhihu.com/p/205192636)
Fast and Deep Facial Deformations:
Skin Deformation Methods for Interactive Character Animation. 2017 Survey for skinning deformation methods:

Chad. https://www.chadvernon.com/tags/maya/

UE PoseWrangle

https://dev.epicgames.com/community/learning/tutorials/r04p/unreal-engine-authoring-secondary-animation-in-maya-and-unreal-with-pose-driver-connect

https://www.unrealengine.com/marketplace/en-US/product/pose-driver-connect?sessionInvalidated=true

如果当前是psd设置为twist，但是有pose是swing得到的，会直接报错
如果权重都为0，就用natrual pose

RBF Solver

是一种非线性插值，样本（以下称Samples）为 $\{X, Y = f(x)\}$

其中 $X = ( x_1,...,x_n), x_i \isin R^{d_1}, Y = (y1, ..., y_n), y_i \isin R^{d_2}$ , n为样本个数

解算出 $f(.)$
对于新输入的一个Query $q \isin R^{d_1}$ , 计算出 $f(q) \isin R^{d_2}$

列举出几种实际应用中的取值

手柄拖动中间的cube移动，移动到四周的每个cube上时，旋转角应当和该处cube相同， $x_i$ 是一个position(d1 = 3), $y_i$ 是对应于Samples每一个样本点的权重（d2=n）
角色动画中，拖动一个手肘关节旋转，次级骨骼随之进行平移/旋转/缩放， $x_i$ 是一个手肘关节的欧拉角(d1 = 3), $y_i$ 是对应于Samples每一个样本点（称为pose）的权重（d2=n）

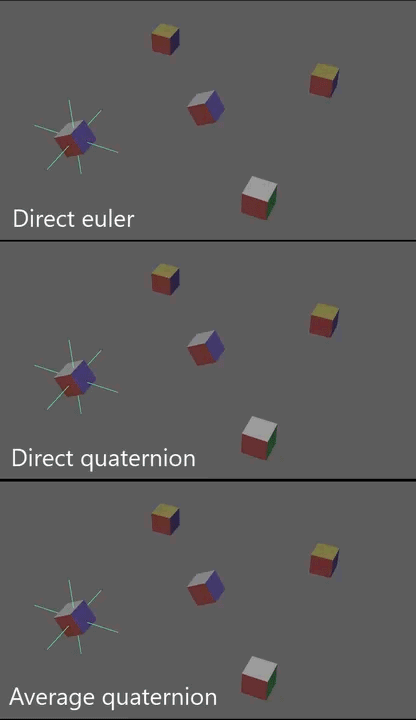
Alt text

可以看出

在应用中一般 d2 == n, 即最终求到的函数值为每一个样本点的权重，比如 $x = x_i时， f(x_i) = [0, 0, ..., 1, 0, ..., 0]$ ，第i位为1，其余为0
$f$ 是一个把 $R^{d_1}$ 映射为 $R^{d_2}$ 的函数，因此可以把 $f$ 看成一个矩阵

A_{d2\times d1} x_{d1 \times 1} = y_{d2 \times 1} \\ \begin{bmatrix} w11 & w12 & ... & w1d_1 \\ w21 & w22 & ... & w2d_1 \\ ... & ... & ... & ... \\ wd_{2}1 & wd_{2}22 & ... & wd_{2}d_1 \\ \end{bmatrix} \cdot \begin{bmatrix} x^1\\ x^2\\ ...\\ x^{d1} \end{bmatrix} = \begin{bmatrix} y^1\\ y^2\\ ...\\ y^{d2} \end{bmatrix}

求解矩阵A的方法： 构建出待求解方程

$D{ij}=Distance(i, j) = ||x_i - x_j||$ (或其他度量距离方式)

\phi_{n\times n} A_{n \times d1} = Y_{n \times d1} \\ \begin{bmatrix} \phi(D_{11}) & \phi(D_{12}) & ... & \phi(D_{1n}) \\ \phi(D_{21}) & \phi(D_{22}) & ... & \phi(D_{2n}) \\ ... & ... & ... & ... \\ \phi(D_{n1}) & \phi(D_{n2}) & ... & \phi(D_{nn})\\ \end{bmatrix} \cdot \begin{bmatrix} w11 & w12 & ... & w1d_1 \\ w21 & w22 & ... & w2d_1 \\ ... & ... & ... & ... \\ wd_{2}1 & wd_{2}22 & ... & wd_{2}d_1 \\ \end{bmatrix} = \begin{bmatrix} y^1_1 & y^1_2 &... & y^1_{d1}\\ y^2_1 & y^2_2 &... & y^2_{d1}\\ ... & ... &... &...\\ y^{d2}_1 & y^{d2}_2 &... & y^{d2}_{d1} \end{bmatrix}

最后的一个矩阵中，每一行是一个样本点（pose）的y，形如[0, 0, ..., 1, 0, ..., 0], 解这个方程可以对A和Y矩阵拆分成列分别来求

\phi_{n\times n} A1_{n \times 1} = Y1_{n \times 1} \\ \phi_{n\times n} A2_{n \times 1} = Y2_{n \times 1} \\ ...\\ \phi_{n\times n} An_{n \times 1} = Yn_{n \times 1} \\

对于每一个形如Ax=b， A为nxn, x为nx1, b为nx1的线性方程组, det(A)!=0时有唯一解，Micchelli定理保证了高斯核时，det(A)!=0，其他情况未保证【这里不确定，没有看过证明】，因此再解算的时候通过

A^TAx=A^Tb

这里 $A^TA$ 一定是对称且正定的，再使用Cholesky分解进行解算。

RBF SDK实现

传入的x(样本) 和 KernalWidth（Sigma）是radiance欧拉角,
计算距离的结果是radiance，计算距离有两种
1. 欧拉角的欧氏距离
2. 四元数的球面角
计算phi(Distance(x)，kernalWidth), 传入的kernalWidth和distance都是radiance的
解算
查询Query 传入radiance欧拉角

总的来说，把RBF SDK作为一个黑箱，输入的都是Radiance，输出的是 0 ~ 1的权重序列

计算距离

template <typename value_t>
struct EuclideanDistMetric : public DistMetricBase<value_t>{
    using vector_t = typename DistMetricBase<value_t>::vector_t;
    value_t eval(const vector_t& A, const vector_t& B) override{
        return (A - B).norm();
    }
};

/// return arc distance in radiance
template <typename value_t>
struct ArcLengthMetric : public DistMetricBase<value_t>{
    using vector_t = typename DistMetricBase<value_t>::vector_t;

    vector_t Euler2Quaternion(value_t roll, value_t pitch, value_t yaw){
        vector_t q(4);
        value_t cy = cos(yaw * 0.5);
        value_t sy = sin(yaw * 0.5);
        value_t cp = cos(pitch * 0.5);
        value_t sp = sin(pitch * 0.5);
        value_t cr = cos(roll * 0.5);
        value_t sr = sin(roll * 0.5);

        value_t w = cr * cp * cy + sr * sp * sy;
        value_t x = sr * cp * cy - cr * sp * sy;
        value_t y = cr * sp * cy + sr * cp * sy;
        value_t z = cr * cp * sy - sr * sp * cy;
        q << x, y, z, w;
        return q;
    }

    value_t eval(const vector_t& A, const vector_t& B) override{
        // Euler to Quaternion
        vector_t A_quat = Euler2Quaternion(A[0],
                                  A[1] ,
                                  A[2] );
        vector_t B_quat = Euler2Quaternion(B[0] ,
                                           B[1] ,
                                           B[2] );
        value_t dotValue = A_quat.dot(B_quat);
        auto ret = acos(2.0 * dotValue * dotValue - 1.0) ;
        return ret;
    }
};

计算phi

/// Linear kernel: (sigma - d) / sigma  if 0 < d < sigma , equal 0 otherwise
template <typename value_t>
struct RBFLinear : public RBFKernelBase<value_t> {
    explicit RBFLinear( value_t sigma) : mSigma(sigma){}


    value_t eval(const value_t &dist) const override {
        auto clamp = [](value_t left, value_t right, value_t x){
            if(x < left) return left;
            else if(x > right) return right;
            else return x;
        };
        return (mSigma - clamp(0, mSigma, dist)) / mSigma;
    }

protected:
    value_t mSigma;
};

/// Exponential kernel: e^(-2 * d / sigma)
template <typename value_t>
struct RBFExponential : public RBFKernelBase<value_t> {
    explicit RBFExponential(value_t sigma) : mSigma(sigma){}


    value_t eval(const value_t &dist) const override {
        return std::exp( -2  * dist / mSigma);
    }

protected:
    value_t mSigma;
};

/// Cubic:  max(1 - d^3 / (sigma^3), 0)
template <typename value_t>
struct RBFCubic : public RBFKernelBase<value_t>{
    explicit RBFCubic(value_t sigma) : mSigma(sigma){}


    value_t eval(const value_t &dist) const override {
        auto value = dist / mSigma;
        return std::max(1 - value * value * value, 0.0);
    }

protected:
    value_t mSigma;
};



/// Gaussian kernel: e^(-d/(sigma*sigma))
template <typename value_t>
struct RBFGaussian : public RBFKernelBase<value_t>
{
    RBFGaussian( const value_t& sigma)
        : mSigma( sigma )
    {}


    value_t
    eval( const value_t& dist ) const
    {
        return std::exp( -dist / (mSigma * mSigma) );
    }
    
protected:
    value_t mSigma;
};

大概是这几个函数

AutoWidth

所有的pose计算两两之间的距离，在求平均值。

计算Phi矩阵

template <typename value_t>
void
RBFSolverBase<value_t>::computeBasisMatrix( matrix_t& basisA ) const
{
    // A matrix of kernel weights
    basisA.conservativeResize(mSamplesAdded, mSamplesAdded);
    for (int col=0;col<mSamplesAdded;++col)
        for (int row=0;row<mSamplesAdded;++row) {
            value_t dist = mDistMetric->eval(mDataCoords[col], mDataCoords[row]);
            basisA(row,col) = mKernels[col]->eval( dist );
        }
}

解线性系统

matrix_t basisA(mSamplesAdded, mSamplesAdded);
this->computeBasisMatrix( basisA );
// Use Cholesky factorization
mWeights.conservativeResize(mValueDim, mSamplesAdded);
// Ax=b ==> A^T A x = A^T b
Eigen::LLT<matrix_t> solver( basisA.transpose() * basisA );
for (int row=0; row<mValueDim ; ++row) {
    // for each row, b is basisA * [0, 0, .1, 0.., 0]^T = basisA.row(row)
    mWeights.row(row) = solver.solve(basisA.row(row).transpose());
}

Maya Node （骨骼版）

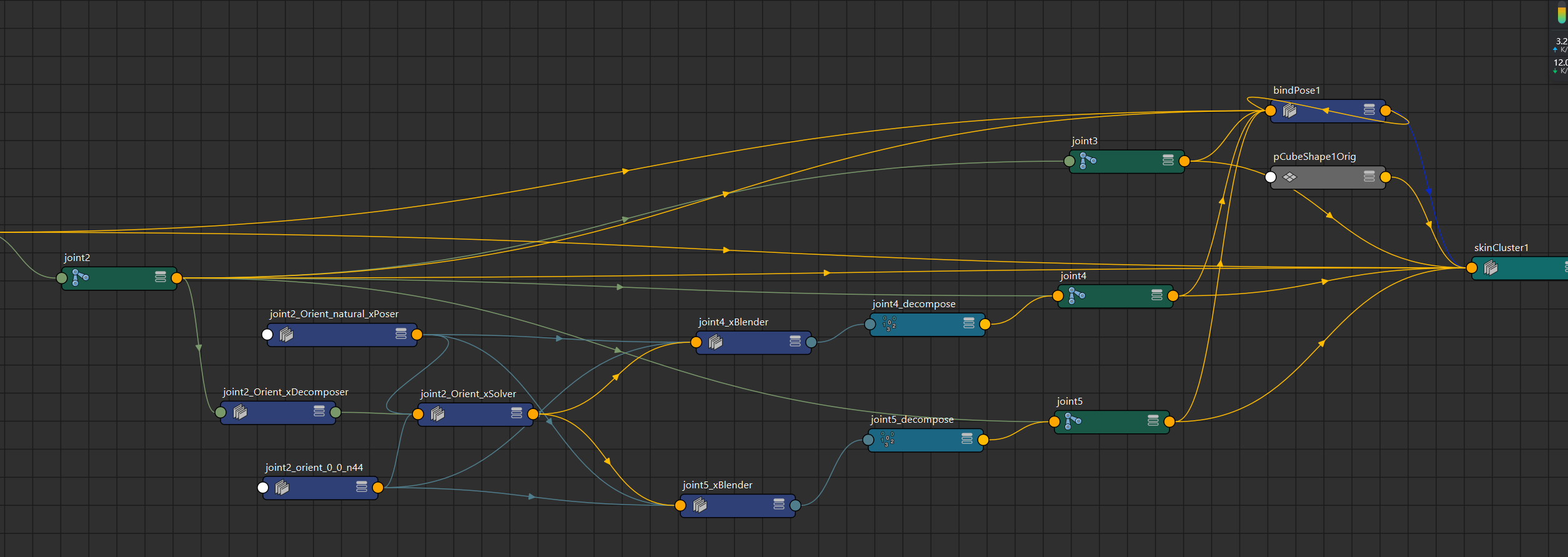
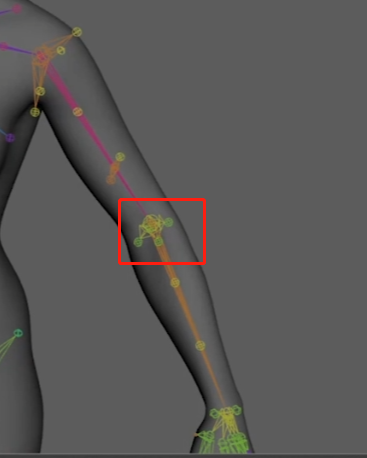
Alt text

技术美术：对于一个既需要swing也需要twist的骨骼，可以采用下面这样的骨骼系统，就可以对两根不同的骨骼绑定两个psd了
- Swing Joint
  - Twist
    - {Twist Driven Joints}
  - {Swing Driven Joints}

之前的方式：通过xDecomposer来指定Orient/Twist，如果是Twist就把joint的rotation关于twist axis的旋转去掉，输出到xSolver; 改为：直接在xSolver中通过距离计算方式来实现【是否考虑twist】

补充上文关于距离计算的方法，额外增加两个：

TwistAngle: 只考虑Twist
SwingAngle：只考虑Swing

计算方法中最核心的部分在于，输入一个四元数q和一个twist axis，将这个q分解为swing和twist两个旋转（keyword: Swing-Twist decomposition for quaternion rotations）参考博客：

// UE中的实现
template<typename T>
T TQuat<T>::GetTwistAngle(const TVector<T>& TwistAxis) const
{
    T XYZ = (T)TVector<T>::DotProduct(TwistAxis, TVector<T>(X, Y, Z));
    return FMath::UnwindRadians((T)2.0f * FMath::Atan2(XYZ, W));
}


vector_t getSwingAngle(const vector_t& q, const vector_t& axis) const {
        vector_t XYZ(3);
        XYZ << q.x(), q.y(), q.z();
        value_t w = q[3];
        vector_t projection = XYZ.dot(axis) * axis;
        vector_t twistQuat(4);
        twistQuat << projection.x(), projection.y(), projection.z(), w;
        if(twistQuat.norm() == 0.f){
            for(int i = 0; i < 3; i++){
                twistQuat[i] = 0;
            }
            twistQuat[3] = 1;
        }else {
            twistQuat.normalized();
        }

        return QuatMultiplyQuat(q, InverseQuat(twistQuat));
}

xDecomposer Node （不方便不好做后续修改）

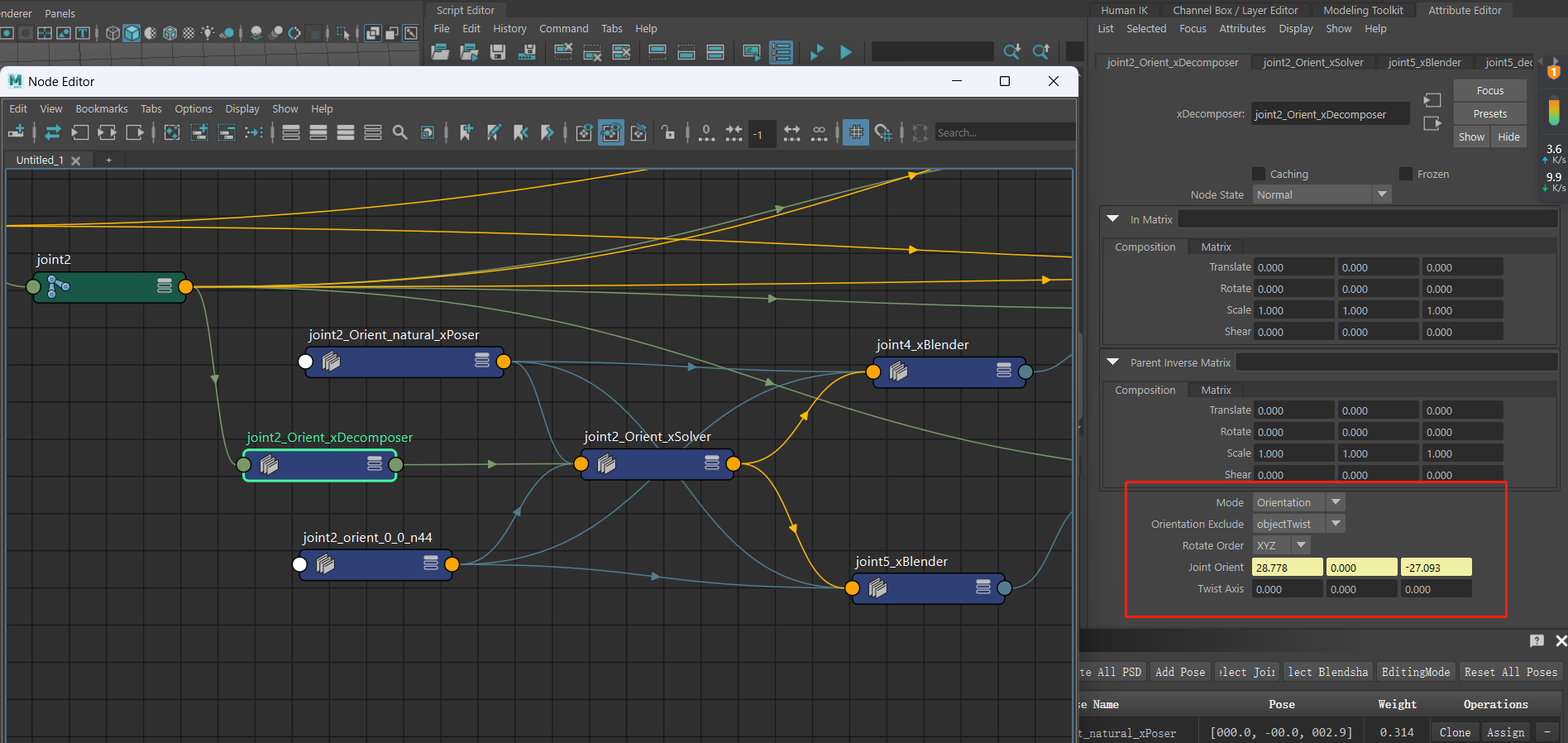
对于Orient psd直接输出joint的欧拉角，对于twist psd根据轴向进行分解 Alt text

输入输出

Input Rotate: Driver joint当前的欧拉角
Output JointOrient:

参数

xSolver Node

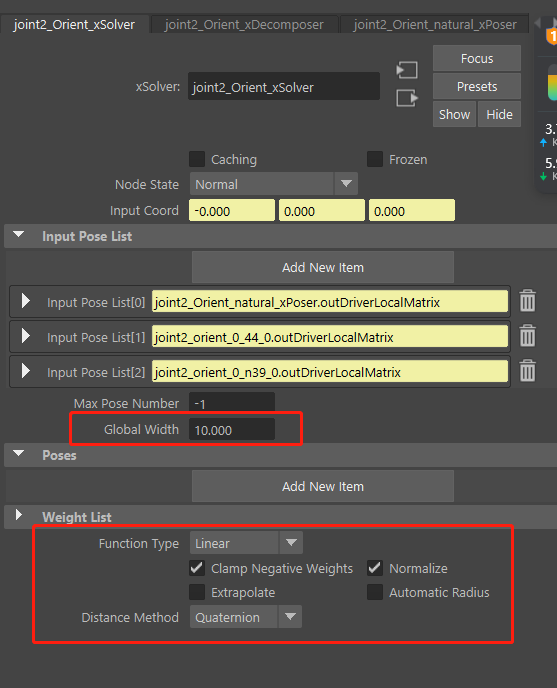
封装了RBF SDK 暴露一些用户自定义参数 Alt text

输入输出

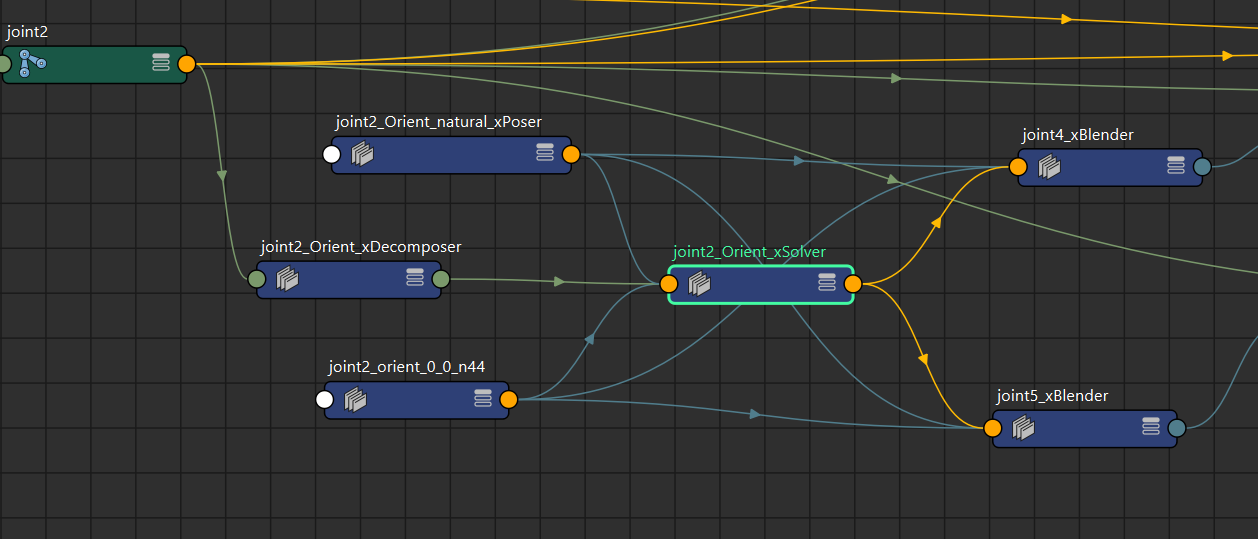
Alt text

InputCoord：当前的Driver的欧拉角 in Degree
InputPoseList：一组【xPoser Node】的输出，每个xPoser表示一个Pose的Driver的Transform矩阵

export psd

UE端插件

json格式

// PSD json格式
{
    "xxx_Solver":{
        "DriverObject" : "arm_l",
        "DrivenObjects" : ["", "", ""],
        "DrivenJointOrientList" : [
            [0, 0, 0],
            [0, 0, 0],
            [-80, 2, 3]
        ],
        "PSDType": 1,
        "BasisFunction": 1,
        "GlobalWidth": 90.0,
        "ClampNegativeWeight": true,
        "NormalizeMethod": 1,
        "TwistAxis": 0,
        "IsAutomaticRadius": true,
        "DistanceMethod": 0,

        "Poses" : {
            "pose_1" : {
                "outDriverLocalMatrix" : [
                    (Mat4x4)
                ],
                "outDrivenLocalMatrixList" : [
                    (Mat4x4),
                    (Mat4x4),
                    (Mat4x4)
                ],
                "RawPoseRotation": [
                    -9.774415372647063e-06,
                    0.00020008505692559357,
                    -119.99999999999999
                ],
            }
        }

    }
}

Max端插件

Max插件

提供四种可选语言：C++,C#, python，maxscript

https://github.com/sideeffects/HoudiniEngineFor3dsMax

官方手册：https://help.autodesk.com/view/MAXDEV/2022/ENU/?guid=Max_Developer_Help_3ds_max_sdk_the_learning_path_getting_started_writing_plug_ins_html

wiki 整理：https://iwiki.woa.com/p/1356062572

参考仓库：https://git.woa.com/DCC_Client/Products/GoSkinning/3dsMax_go_skinning_cplusplus

开发配置

Alt text 使用Release模式其他模式可能编不过 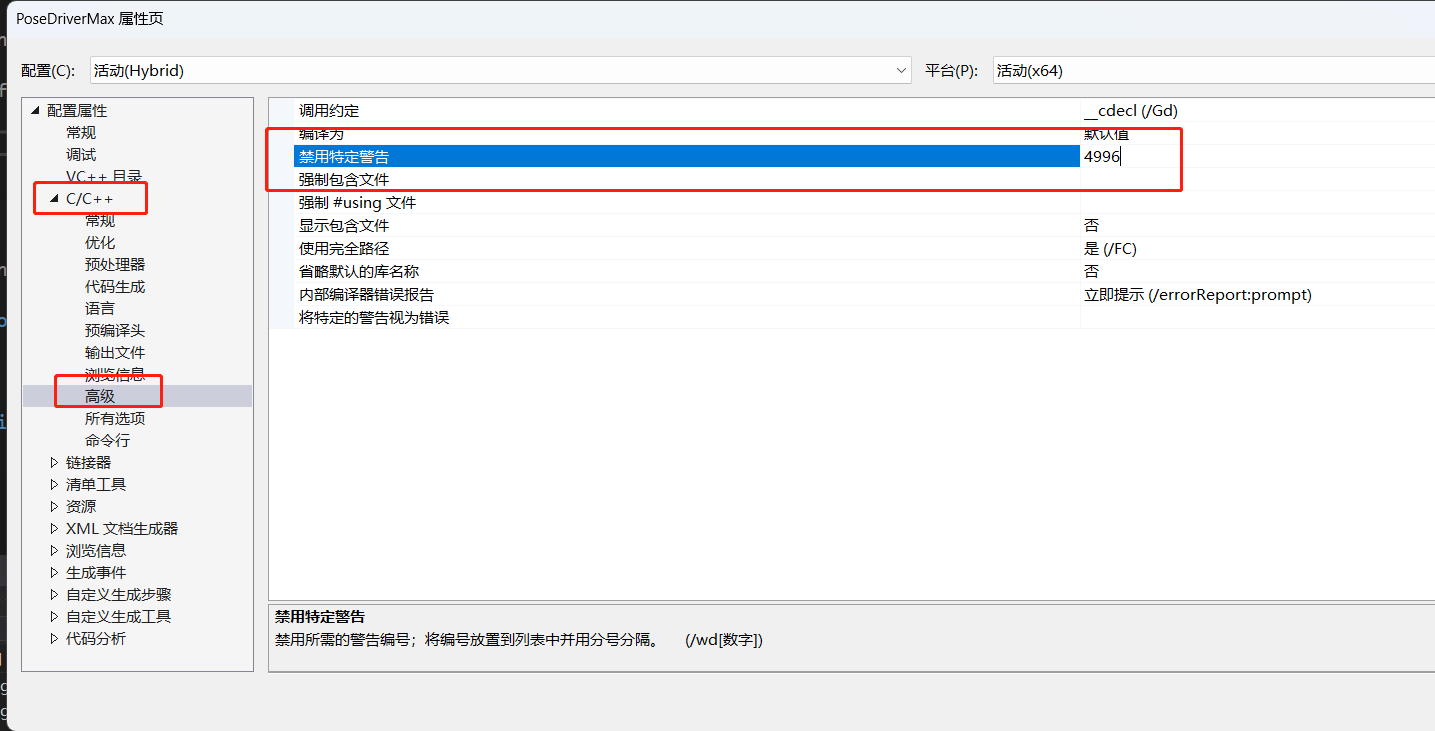include目录 moc生成不了要去generatedfiles下面添加一个release/hybrid目录

使用说明

Matrix Decompose to TRS

在maya中（应该所有的都是这样），一个affine变化对应的TRS顺序应该为，先Scale, 再Rotation，最后Translate。因为Translate对S和R有影响，我们希望S和R的pivot是原点/过原点的轴，所以最后Translate；Scale沿着xyz轴缩放（初始的时候物体的xyz和世界坐标对齐），所以先Scale。

如何分解？

https://math.stackexchange.com/questions/237369/given-this-transformation-matrix-how-do-i-decompose-it-into-translation-rotati

// Decompose a matrix into TRS
// 如果存在shear 就需要polar decompose
// 存在shear  == 缩放的轴和物体局部坐标系的轴没有对齐 == 先进行了旋转再进行了缩放（世界坐标系的缩放）
// 但是在maya中拖动手柄进行的缩放操作都是按照局部坐标系操作的（等价于先缩放再旋转） ==> 不会有shear

// 参考UE中的FTransform(TMatix) 中会对TMatrix进行ExtractScaling (伪代码) trans = mat.GetTrans(); scale = vec3{mat[0][0:3].norm(), mat[1][0:3].norm(), mat[2][0:3].norm()}; rot = mat[0 : 3][0 : 3] / scale;

// 在3ds Max API中有DecomposeMatrix（）函数对TRS顺序的Matrix进行分解

### ue插件文件结构
```cpp
// 做一些省略，不区分Private和Public，省略文件名字的XPoseDriver前缀

- XPoseDriverEditor
    // 蓝图相关
    - BPLibrary.h
    - BPLibrary.cpp 

    // 自动生成的？
    EditorModule.h
    EditorModule.cpp

    // 继承UAnimGraphNode_Base
    UAnimGraphNode_XPoseDriver.h
    UAnimGraphNode_XPoseDriver.cpp

- XPoseDriverRuntime
- ThirdParty
    - include / xPsd.h
    - lib / XPsdLib.lib

使用说明

通过distance method来制作swing和twist psd

distance method是一个psd的属性，一个psd要么是swing要么是twist，对比三种distance method方法。可以对同一个joint分别建swing和twist两个psd。

Euclidean：两个pose的欧拉角的欧氏距离，会混合swing轴向和twist轴向的影响
Quaternion：四元数在球面上的夹角，会混合swing轴向和twist轴向的影响
Swing：四元数在球面上的夹角在非twist轴向的分量，不会包含twist
Twist：四元数在球面上的夹角在twist轴向的分量，只会包含twist

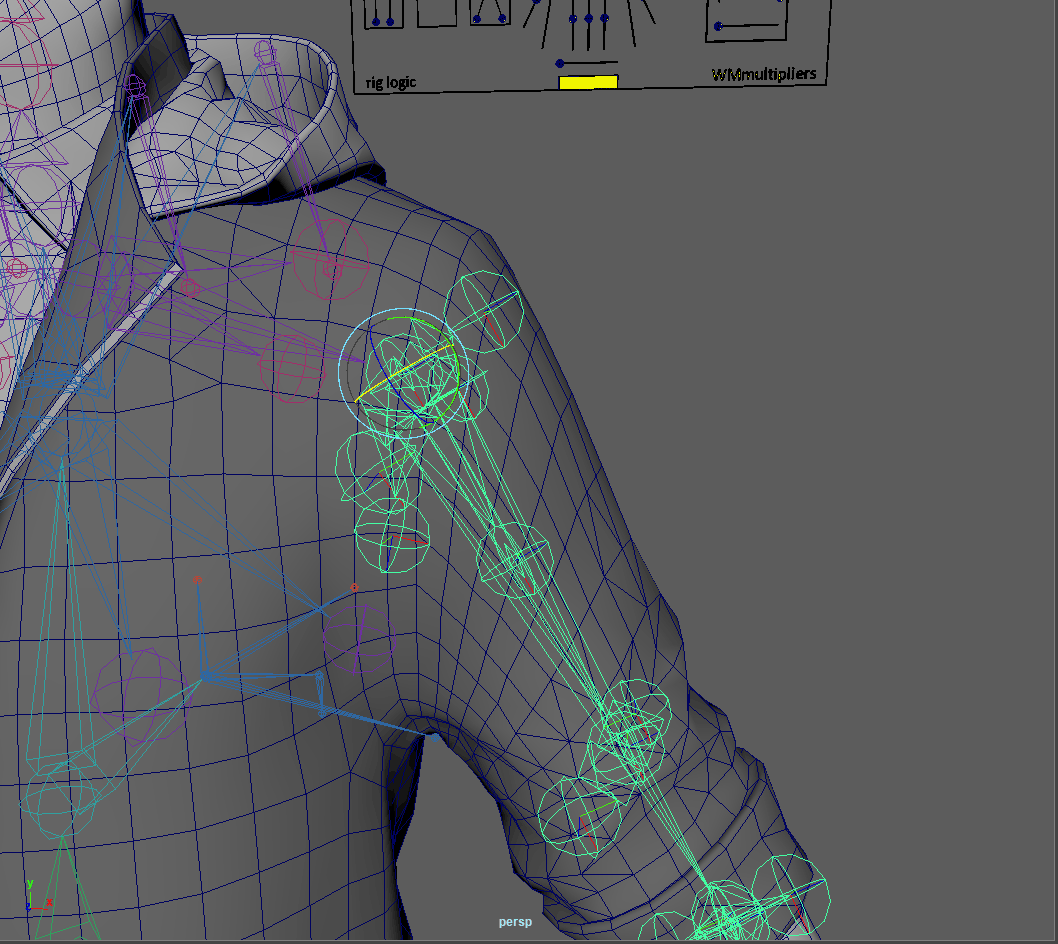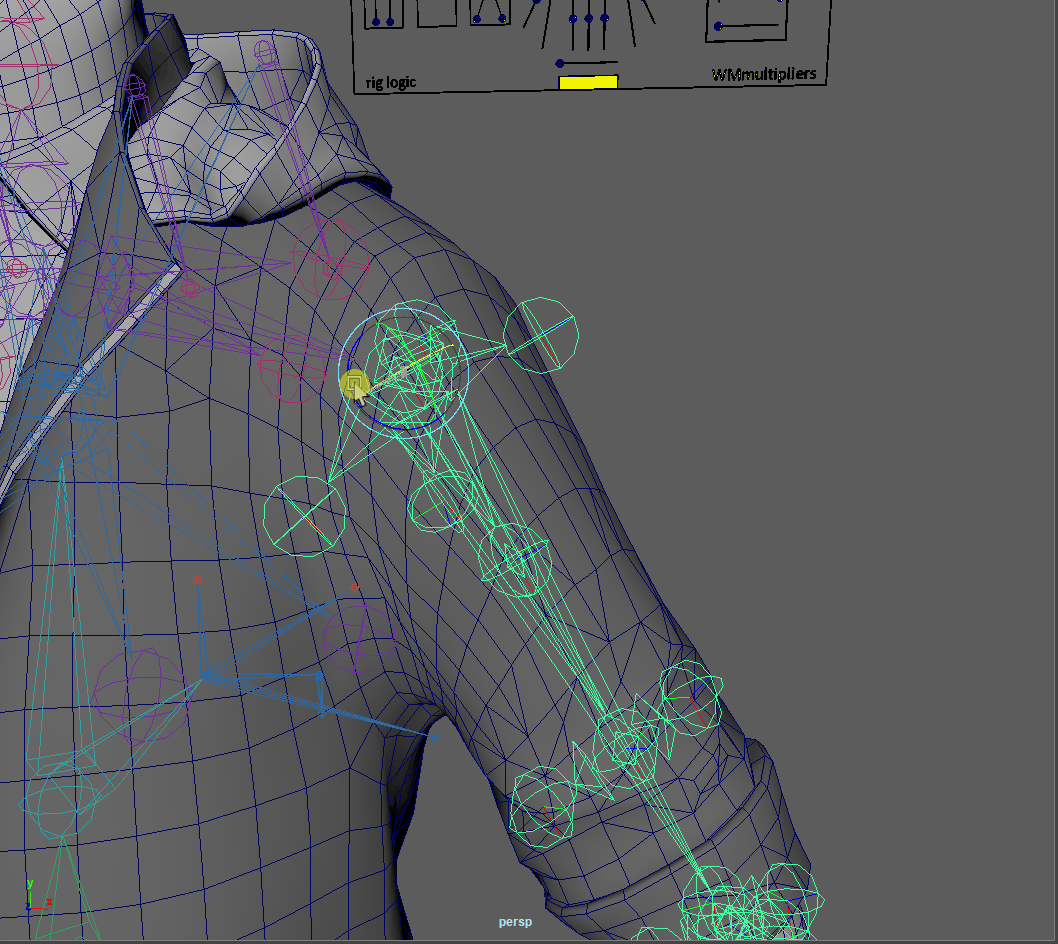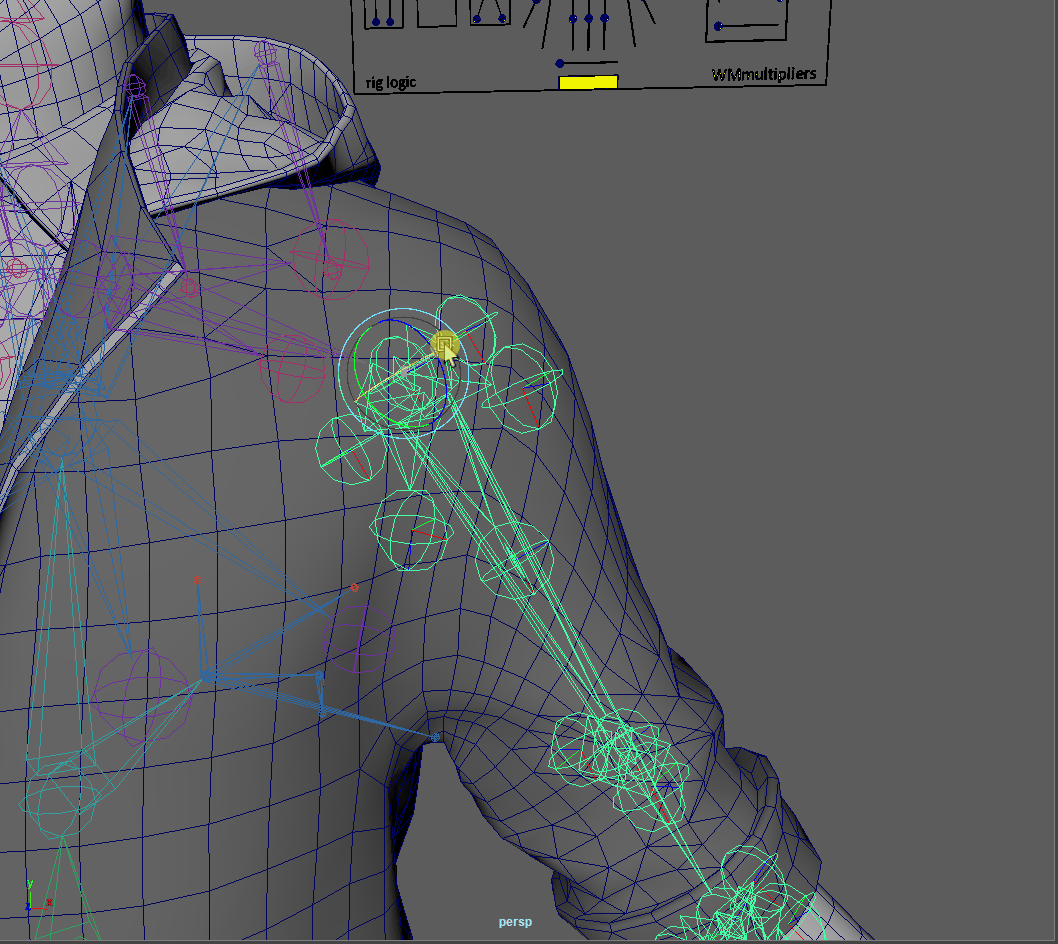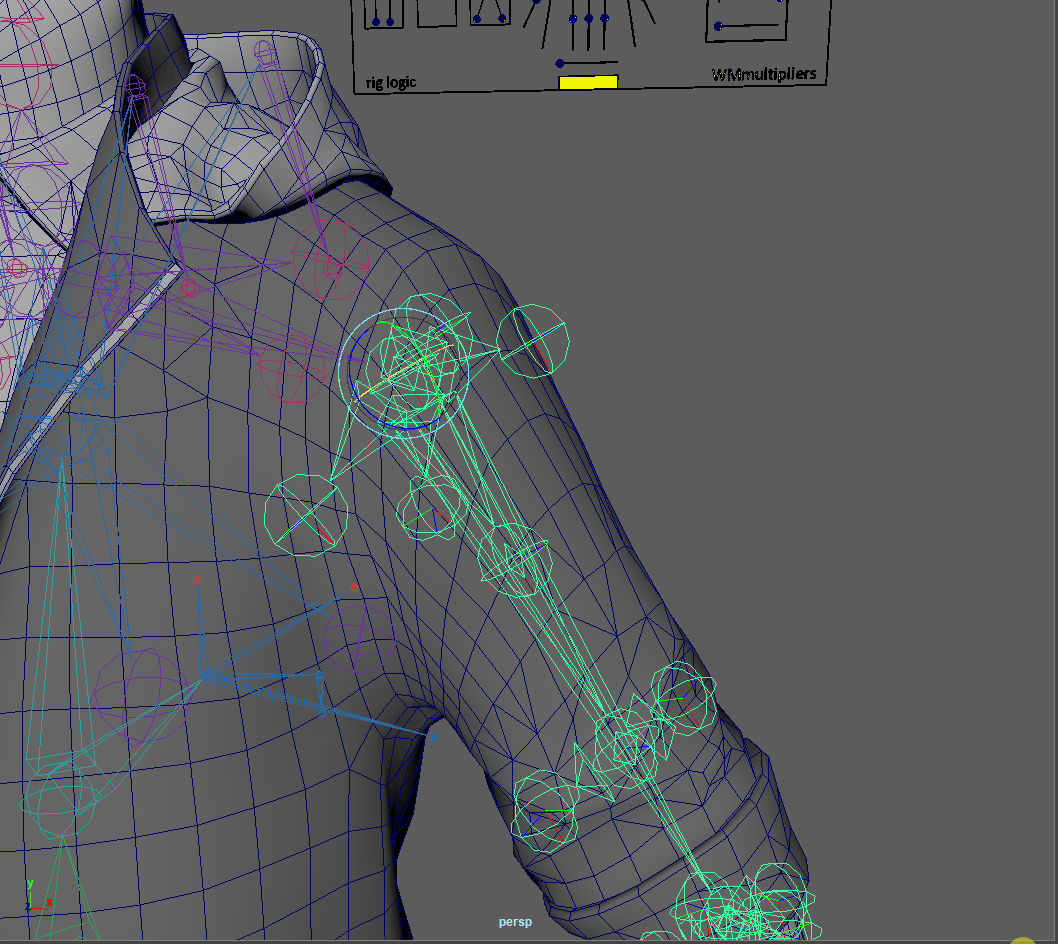
Euclidean Alt text

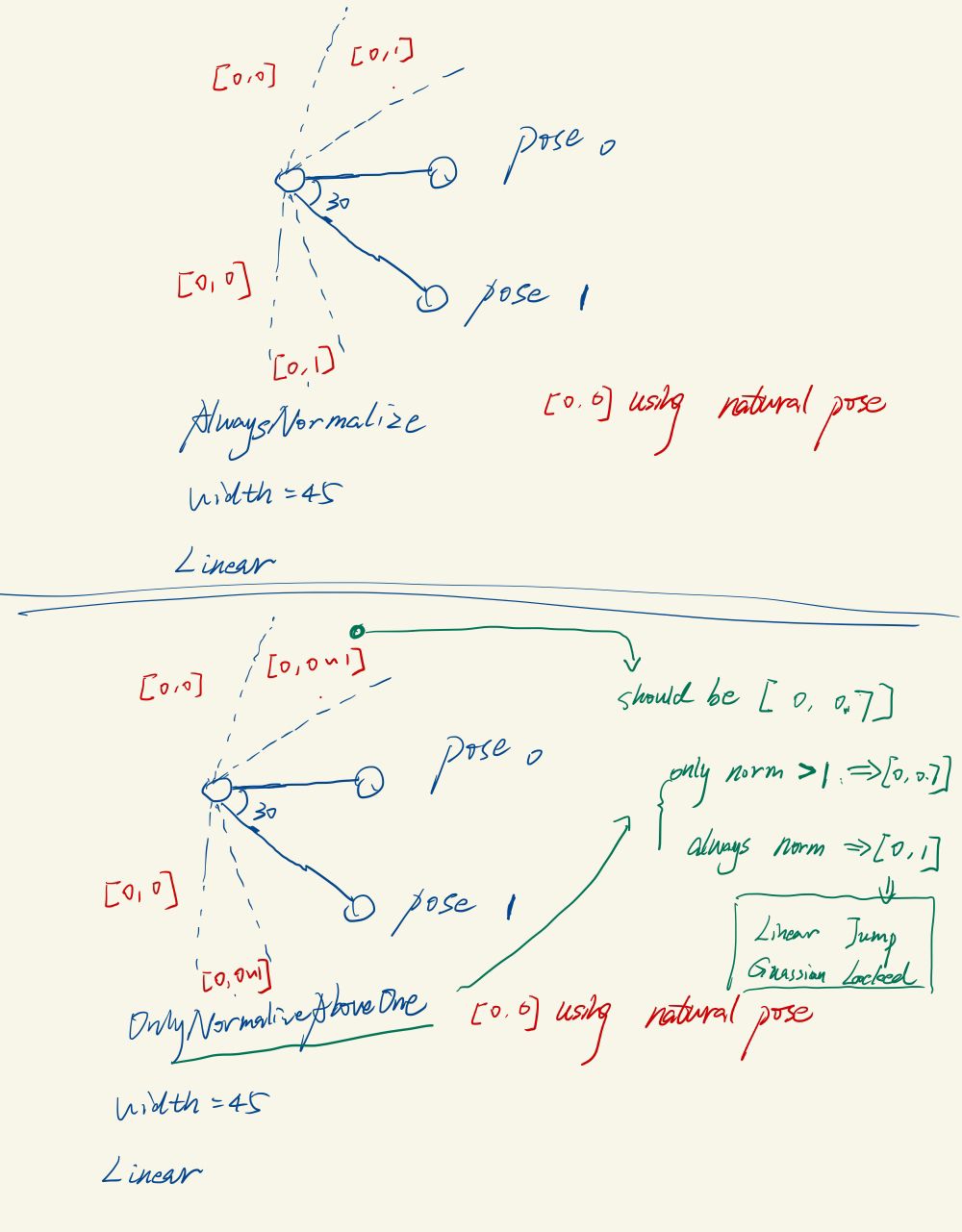
Swing Alt text

Twist Alt text

width和normalize method

width: 用来控制每个pose的影响范围，如果核函数是Linear，离某个pose超过width范围时，该pose影响立刻变为0；而若采用Guassian核则会在超过pose后平滑递减直至0
normalize methd
- OnlyNormalizeAboveOne: 对最外侧pose继续向外旋转会让权重逐渐下降(此时权重和会小于0，比如权重列表为[0, 0, ...,0, 0.7])
- AlwaysNormalize：对最外侧pose继续向外旋转会让权重保持（权重会一直为[0, 0, ..., 1]）
额外后处理：若所有pose的影响都为0，自动跳转到natural pose

Alt text

概要​

调研技术方案​

UE PoseWrangle​

RBF Solver​

RBF SDK实现​

计算距离​

计算phi​

AutoWidth​

计算Phi矩阵​

解线性系统​

Maya Node （骨骼版）​

xDecomposer Node （不方便 不好做后续修改）​

输入输出​

参数​

xSolver Node​

输入输出​

export psd​

UE端插件​

json格式​

Max端插件​

Max插件​

开发配置​

使用说明​

Matrix Decompose to TRS​

使用说明​

通过distance method来制作swing和twist psd​

width和normalize method​

概要

调研技术方案

UE PoseWrangle

RBF Solver

RBF SDK实现

计算距离

计算phi

AutoWidth

计算Phi矩阵

解线性系统

Maya Node （骨骼版）

xDecomposer Node （不方便不好做后续修改）

输入输出

参数

xSolver Node

输入输出

export psd

UE端插件

json格式

Max端插件

Max插件

开发配置

使用说明

Matrix Decompose to TRS

使用说明

通过distance method来制作swing和twist psd

width和normalize method